Hidrotec - Uma ferramenta para o planejamento e gestão dos recursos hídricos no Estado de Minas Gerais

METODOLOGIAS UTILIZADAS NO DESENVOLVIMENTO DO “ATLAS DIGITAL DAS ÁGUAS DE MINAS” (E CONSIDERAÇÕES GERAIS SOBRE OS RESULTADOS)

SUMÁRIO:

A) METODOLOGIAS UTILIZADAS

1) Metodologias de regionalização hidrológica

1.1) Metodologia de regionalização da vazão mínima, máxima e média de longo período

1.2) Metodologia de regionalização da curva de permanência

1.3) Metodologia de regionalização de curvas de regularização

2) Metodologia de mapeamento de variáveis e funções hidrológicas

3) Sistema Simplificado de Apoio a Gestão das Águas – SAGA

3.1) Consulta espacial georreferenciada

Informações hidrológicas na rede hidrográfica
Informações em qualquer seção fluvial
Modelos hidrológicos ajustados por cursos d’água
Nascentes com informações hidrológicas
Imagens de satélite
Balanço demanda/disponibilidade por bacia
Regiões hidrologicamente homogêneas
Rede hidrológica georreferenciada com informações de vazão e precipitação pluvial

3.2) Consulta informativa

Balanço hídrico nas sub-bacias
Contribuição dos afluentes principais
Comportamento hidrológico no rio principal
Comportamento hidrológico da vazão máxima
Disponibilidade hídrica nas sub-bacias
Disponibilidade hídrica per capita
Índice de vazões mínimas
Impacto ambiental relevante
Modelos de vazões ajustados nas regiões hidrologicamente homogêneas
Mapas de vazões específicas
Mapas de precipitação pluvial
Rios com baixa capacidade de regularização natural
Resumo expandido

4) Validação das metodologias desenvolvidas no ATLAS

B) CONSIDERAÇÕES GERAIS SOBRE OS RESULTADOS

A) METODOLOGIAS UTILIZADAS

As metodologias, ora apresentadas, correspondem à experiência adquirida nos estudos de regionalização hidrológica no âmbito do Programa HIDROTEC, realizados nas regiões hidrográficas mineiras e partes das regiões dos Estados do Espírito Santo, Bahia, Goiás e Distrito Federal abrangendo uma área de 1.986.000 km², além de outras, fora do Estado, como a bacia do rio Purus, na região Amazônica.

No decorrer desta experiência, foi desenvolvido um programa computacional de regionalização hidrológica, RH, o qual sintetiza a metodologia de regionalização, atualmente, na versão RH4.0. Trata-se de ferramenta eficiente em estudos de quantificação de recursos hídricos, possibilitando obter as variáveis e funções hidrológicas, de forma simples e rápida, em base científico-tecnológica, consoante com a agilidade que as decisões, no âmbito da administração dos recursos hídricos, requerem.

As disponibilidades e potencialidades hídricas estão representadas pelas variáveis e funções hidrológicas: vazão mínima de sete dias de duração e período de retorno de 2, 5 e 10 anos com intervalo anual; vazão mínima de sete dias de duração e período de retorno de 10 anos com intervalo sazonal (período seco – abril/setembro e período chuvoso – outubro/março), vazão mínima com permanência de 50, 75, 85, 90 e 95%, vazão média de longo período, vazão máxima diária anual para os períodos de retorno de 2, 10, 20 50, 100 e 500 anos, vazão máxima possível de ser regularizada através de barramentos, vazão máxima possível de ser regularizada e disponibilizada para outorga à jusante do barramento, volume de armazenamento necessário a regularização da vazão máxima possível de ser regularizada, volume de armazenamento necessário a regularização da vazão mínima residual (70% da Q_7,10) e volumes de regularização em reservatórios em função da vazão de interesse a ser regularizada.

As vazões mínimas, como a de sete dias de duração e período de retorno de 10 anos (Q_7,10), e as obtidas da curva de permanência para 90 e 95 % de probabilidade (Q₉₀ e Q₉₅) são valores característicos do comportamento da estiagem em uma bacia hidrográfica, enquanto a vazão média de longo período (Qmlp), corresponde a síntese de todas as vazões ao longo do tempo. A vazão Q_7,10 apresenta um enfoque estatístico pois é considerada como variável aleatória à qual se aplica técnicas estatísticas para avaliar sua probabilidade de ocorrência. Corresponde a um valor que, em média, a cada 10 anos, será igualado ou inferiorizado pelo escoamento médio de estiagem do rio em quaisquer 7 dias consecutivos. A curva de permanência de vazões é uma tradicional função hidrológica e por isso as vazões Q₉₀ e Q₉₅ dela extraídas têm enfoque hidrológico. A curva de permanência fornece a porcentagem de tempo que uma dada vazão é igualada num período histórico definido.

Estas três modalidades de vazões são utilizadas em vários Estados brasileiros como "vazão de referência", para definição de critérios de outorga de direito de uso de água . Por exemplo, nos Estados de Minas Gerais, São Paulo, Rio de Janeiro, Espírito Santo e Paraná utilizam a vazão Q_7,10. Já vários Estados situados no nordeste como: Bahia, Pernanbuco, Paraíba, Rio Grande do Norte, Ceará e o Estado de Goiás adotaram as vazões Q₉₀ e Q₉₅. Em Minas Gerais, de acordo com a portaria 010/98 do Instituto Mineiro de Gestão da Água-IGAM é fixado o percentual de 30% da Q_7,10 como limite máximo de derivações consuntivas a serem outorgadas, em cada seção da bacia hidrográfica considerada, garantindo, assim, vazões residuais mínimas, a jusante, equivalentes a 70% da Q_7,10. Informações mais detalhadas sobre os procedimentos estatísticos de estimativa da vazão Q_7,10 encontram-se no tópico 1.1 (Metodologia de regionalização da vazão mínima, máxima e média de longo período). Já para as vazões Q₉₀ e Q₉₅ os procedimentos hidrológicos encontram-se no tópico1.2 (Metodologia de regionalização da curva de permanência). É oportuno mencionar que a vazão Q₉₅ é freqüentemente utilizada no dimensionamento de pequenas centrais hidréletricas - PCHs.

Considerando a significativa diversidade hidrológica que ocorre em território mineiro, e certamente a necessidade de se aperfeiçoar, num futuro próximo, estudos de vazões de referência diferenciadas para algumas regiões hidrográficas do Estado, as três modalidades de vazões Q_7,10, Q₉₀ e Q₉₅ foram quantificadas em todas as regiões hidrográficas estudas no âmbito do programa HIDROTEC. O mesmo procedimento foi adotado para a vazão mínima de sete dias de duração e período de retorno de 10 anos com intervalo sazonal (período seco – abril/setembro e período chuvoso – outubro/março).

A maioria das técnicas utilizadas em estudos hidrológicos depende, para sua aplicação, de dados confiáveis a respeito do volume de água precipitado ou evaporado, e da vazão dos cursos d’água. Estas informações são obtidas em estações fluviométricas e pluviométricas distribuídas nas regiões hidrográficas. Portanto, o estabelecimento de uma rede hidrológica e a sua manutenção ininterrupta, ao longo do tempo, são condições absolutamente necessárias ao estudo hidrológico.

Os levantamentos de informações pluvio-fluviométricas tiveram início, há mais de cem anos, quando foram instaladas as primeiras estações pluviométricas com medições regulares e, também, iniciadas as primeiras estações com controles de níveis e medições de vazões, objetivando fazer face, já naquela época, às necessidades de aproveitamento da energia hidráulica.

A precipitação é medida como a altura de água ou lâmina que seria acumulada em superfície plana, se nenhuma perda ocorresse. O aparelho usado para esta medição é o pluviômetro ou pluviógrafo. O pluviômetro marca o total acumulado, em um dado período de tempo, sendo sua leitura realizada, em geral, uma vez por dia, às 7 ou às 9 horas. O pluviógrafo registra, continuamente, a precipitação em um local. É utilizado quando se faz necessário o conhecimento da distribuição temporal da precipitação e da variação de sua intensidade.

De modo geral, a vazão é obtida a partir do nível das águas, através do uso de régua linimétrica ou por instrumentos de registro contínuo, os linímetros ou linígrafos. Estes aparelhos registram, continuamente, as variações de nível d’água, ao longo do tempo, na seção de controle. As leituras em réguas linimétricas são, em geral, realizadas duas vezes por dia em horas fixas. Uma vez obtida a série de níveis, transforma-se a série de nível em série de vazão através do uso da curva-chave daquela seção, a qual relaciona nível-vazão.

O levantamento de dados hidrológicos, pela sua importância, está despertando interesse do mercado para o desenvolvimento e disponibilização de novos equipamentos de hidrometria para coleta, armazenamento e transmissão de dados, facilitando o trabalho de campo e aumentando a confiabilidade das informações levantadas. O caráter estratégico das informações hidrológicas foi o elemento decisivo para que a Agência Nacional de Águas – ANA, assumisse, de fato, a partir de janeiro de 2003, a administração da operação e manutenção da rede básica de estações hidrometeorológicas em todo território brasileiro.

De acordo com o Sistema Nacional de Informações sobre Recursos Hídricos-SNIRH/ANA, estão em operação no País, através de diversas entidades, cerca de 8.760 estações pluviométricas e 4.133 fluviométricas. Das estações fluviométricas, 948 tem monitoramento de qualidade de água e 537 tem medições sedimentométricas.

É importante resaltar que nos estudos de regionalização hidrológica realizadas nas regiões hidrográficas mineiras, incluindo aí, a área baiana compreendendo as bacias do Leste, rios Pardo e Jequitinhonha e a área capixaba da bacia do rio Doce, foram utilizadas 318 estações fluviométricas, apresentando, assim, uma densidade de 1: 1.846 km². Relativamente ao número de estações pluviométricas, foram utilizadas 378 estações, com uma densidade de 1: 1.553 km².

Uma rede hidrológica de informação, dificilmente, cobre todos os locais de interesse para o desenvolvimento e conservação dos recursos hídricos. Sempre existirão lacunas temporais e espaciais que necessitam ser preenchidas com base em metodologias robustas.

As metodologias utilizadas para estimativa das vazões dos cursos d’água dependem, para sua aplicação, de dados confiáveis a respeito da quantidade e qualidade das informações hidrológicas, disponíveis na região hidrográfica de interesse.

De um modo geral, a estimativa da vazão pode ser realizada: a) diretamente, utilizando-se as séries históricas de vazões registradas em estações fluviométricas ou, b) indiretamente, através de dados de precipitação pluvial. Na primeira opção (a), a estimativa está, diretamente, relacionada com a distribuição espacial das estações hidrométricas na rede hidrográfica. Neste caso, têm-se, praticamente, três situações:

1. Local de interesse coincide com o local da estação fluviométrica

Procedimento: Ajustar uma distribuição de probabilidades à série histórica dos dados de vazão

(Várias curvas ou distribuições têm sido propostas para interpretar as séries históricas de vazões. Usualmente, seleciona-se uma família de curvas mais indicadas ao tipo de dados analisados e, a seguir, seleciona-se a distribuição por meio da aplicação de um teste de aderência como, por exemplo, Kolmogorov-Smirnov, qui-quadrado ou graficamente. As distribuições de probabilidades mais utilizadas para representar os eventos máximos são Gumbel, log-normal II, Pearson tipo III e log- Pearson tipo III e, para os mínimos, Weibull, log-normal III, log-Gumbel, Pearson tipo III e log- Pearson tipo III).

2. Local de interesse se encontra próximo de uma (ou mais) estação(ões) fluviométrica(s)

Procedimento: Realizar a transferência espacial de informações por meio da aplicação de técnicas usuais de transferência

(As técnicas usuais são: a)- transferência da vazão proporcionalmente à respectiva área de drenagem (vazão específica constante.); e b)- interpolação linear entre duas ou mais estações proporcionalmente às respectivas áreas).

OBS: Considerando-se que o escoamento superficial em uma bacia hidrográfica é um processo não-linear, recomenda-se que a diferença (valor absoluto) entre as áreas das bacias de drenagem do local de interesse e a da estação fluviométrica não supere 30% da área de influência da estação. É recomendável, também, que as estações, preferencialmente, estejam inseridas na mesma calha fluvial e numa região com comportamento hidrológico semelhante.

3.Local de interesse se encontra distante das estações fluviométricas

Procedimento: Aplicar técnicas de regionalização hidrológica

(Empregar modelos de cálculo de vazões estatisticamente ajustados e aplicáveis à qualquer seção fluvial da bacia hidrográfica).

A segunda opção(b) apresenta a alternativa de se estimar a vazão, indiretamente, utilizando-se dados de precipitação pluvial. Neste caso, pode-se aplicar: a)- métodos classificados como empíricos, tais como: o método racional, o hidrograma unitário e o método da curva-índice; b)- transferência de informações pluviométricas com base na área de drenagem da bacia; e c)- modelos matemáticos de simulação do processo de transformação chuva-vazão, calibrado, individualmente, para cada bacia, onde estejam disponíveis registros simultâneos de chuva, vazão-evaporação ou evapotranspiração e parâmetros ou variáveis, tais como: capacidade de infiltração, estado de umidade do solo, nível dos aqüíferos, dentre outros.

A metodologia, compreendendo a utilização de séries históricas de vazões registradas em estações fluviométricas, deve ser a preferida sempre que existirem dados de vazão em quantidade adequada. A vantagem em relação a segunda opção é a eliminação das incertezas da transformação de dados de chuva em vazão.

Como o Brasil é um país de grande extensão territorial, com uma rede hidrométrica esparsa, a estimativa das vazões dos cursos d’água constitui um problema sério, pois o conhecimento dessas vazões é fundamental em hidrologia. Para suprir a deficiência da rede hidrométrica, uma técnica que tem apresentado resultados satisfatórios é a regionalização hidrológica.

Em sentido amplo, entende-se por regionalização hidrológica qualquer processo de transferência de informações, de um local para outro, dentro de uma área de comportamento hidrológico semelhante. Essas transferências podem abranger, diretamente, as séries de vazões e, ou, precipitações ou determinados parâmetros estatísticos relevantes tais como: média, variância, máximos e mínimos e, ainda, equações e parâmetros relacionados com estas estatísticas.

Em sentido mais restrito, a regionalização hidrológica significa apenas as duas últimas formas de transferência, isto é, equações e parâmetros relacionados com as estatísticas, sendo suficiente para se obterem resultados em qualquer ponto de toda uma região. A transferência de séries de vazões ou precipitações é denominada, simplesmente, transferência de informações e se restringe a locais particulares.

A regionalização hidrológica possibilita a obtenção de variáveis hidrológicas básicas, como vazões máximas, mínimas, média de longo período, curva de permanência e curvas de regularização de maneira simples e rápida, de acordo com a agilidade que a administração dos recursos hídricos requer para suas decisões. Além disso, a estimativa dos valores das variáveis hidrológicas, para uma determinada bacia, baseada nos parâmetros regionais, parece ser, geralmente, mais razoável que a obtida a partir de uma única série observada em outro local.

Sendo um instrumento eficaz, em estudos de planejamento e administração de recursos hídricos, a regionalização também pode ser usada para melhorar as amostras pontuais e, em conseqüência, melhorar as estimativas das variáveis hidrológicas; verificar a consistência das séries hidrológicas e identificar a falta de postos de observação.

Dentre os métodos de regionalização hidrológica baseados na técnica de regressão múltipla citam-se:

a)	Métodos que regionalizam a vazão com um determinado risco;
b)	Métodos que regionalizam uma curva de probabilidade adimensional e o fator de adimensionalização;
c)	Métodos que regionalizam funções específicas; e
d)	Métodos que regionalizam parâmetros de uma distribuição estatística ou parâmetros de modelos hidrológicos.

Outros procedimentos alternativos de apoio à regionalização são a correlação entre vazão e precipitação pluvial e o uso de indicadores regionais.

Em regiões hidrográficas, onde os dados planialtimétricos já se encontram na forma digital, a utilização de SIG, através da aplicação do modelo digital de elevação na estimativa dos parâmetros e variáveis hidrológicas otimiza, substancialmente, o processo de regionalização.

1) METODOLOGIAS DE REGIONALIZAÇÃO HIDROLÓGICA

Por meio da aplicação da técnica de regionalização hidrológica com base nos dois primeiros métodos (a e b), citados anteriormente e utilizando-se o programa computacional de regionalização hidrológica RH versão4.0, será possível aprofundar-se no conhecimento das relações entre as variáveis hidrológicas com as características físicas e climáticas da bacia, permitindo-se, assim, compreender e reproduzir melhor o comportamento da bacia.

1.1) METODOLOGIA DE REGIONALIZAÇÃO DE VAZÕES MÍNIMAS, MÁXIMAS E MÉDIAS DE LONGO PERÍODO

A metodologia a ser utilizada para vazões mínimas, máximas e médias de longo período consiste, basicamente, na utilização de dois critérios para identificar as regiões hidrologicamente homogêneas, relativamente às vazões estudadas em uma bacia hidrográfica, e na aplicação de dois métodos de regionalização de vazão.

Como os trabalhos de regionalização das vazões mínimas, máximas e média de longo período apresentam etapas comuns, a descrição destas etapas são apresentadas, segundo o fluxograma geral mostrado na Figura 1 (EUCLYDES et al., 1999).

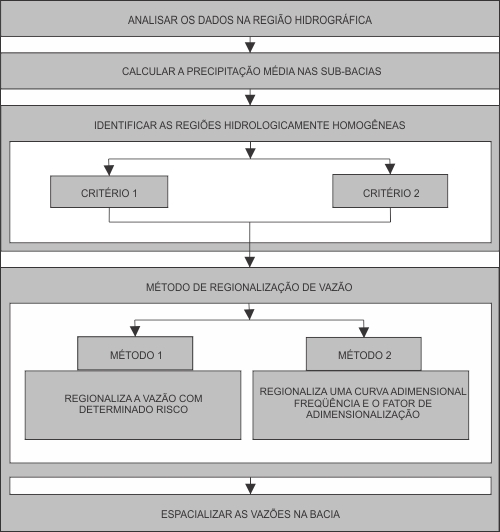Figura 1 - Fluxograma geral da metodologia de regionalização de vazão.

Primeira etapa: Análise dos dados descritivos, hidrológicos e físicos das bacias

Com base nas informações existentes em estudos anteriores e nas informações locais, serão identificados dados descritivos, tais como: cursos d’água principais e seus afluentes, cobertura vegetal, relevo geral, formação geológica, hidrogeologia, distribuição climática, principais aproveitamentos da água e interferências de finalidade, etc.

Os dados hidrológicos serão selecionados através dos inventários das estações fluvio-pluviométricas, disponibilizados pela Agência Nacional das Águas-ANA. Considerando-se que os dados de vazão e precipitação já foram consistidos pela ANA, a análise a ser realizada terá por objetivo a eliminação de erros grosseiros, pontuais, ou incoerências nos dados. Aos dados considerados inconsistentes serão atribuídas falhas, para posterior preenchimento.

Objetivando verificar as possíveis interferências nas séries históricas das vazões dos cursos d’água, devido à existência de barragens à montante das estações fluviométricas selecionadas, serão aplicados testes paramétricos nas séries históricas para aquelas estações localizadas próximas às barragens existentes. As estações em que a operação do reservatório alterar significativamente a variância da série de vazões serão descartadas.

Nas estações fluviométricas em que houve mudança de seção de medição de descarga para locais próximos, no mesmo curso d’água e praticamente com a mesma área de drenagem, serão também aplicados testes paramétricos nas séries históricas das referidas estações com o objetivo de verificar a possibilidade de considerar as duas séries como pertencentes a uma única estação ou sub-bacia.

O preenchimento de falhas e a extensão das séries serão realizados por meio de correlações, segundo critérios consagrados de escolha de bases para as regressões. No caso de vazões, o preenchimento de falhas será realizado somente para as estações mais próximas e localizadas na mesma calha fluvial. Será adotado como valor do coeficiente linear de correlação R2 ≥ 0,90.

Para o preenchimento de falhas de vazão será utilizado a regressão linear simples e a potencial conforme recomendado por EUCLYDES et al. (1999). As equações adotadas serão:

(1.1)

(1.2)

em que

y - é a vazão do posto com falhas;

x - é a vazão do posto com dados;

B₀ e B₁- são parâmetros ajustados na regressão.

No preenchimento de falhas em série pluviométrica, será utilizado o método de ponderação regional com base em regressões lineares, conforme apresentado por BERTONI e TUCCI (1993). Consiste em estabelecer regressões lineares entre o posto com dados a serem preenchidos, Y, e cada um dos postos vizinhos, X₁ X₂, ... , X_n. De cada uma das regressões lineares efetuadas obtém-se o coeficiente de correlação r, e estabelecem-se fatores de peso, um para cada posto. A expressão fica:

(1.3)

em que

W_xj - fator de peso entre os postos Y e Xj;

r_yxj - coeficiente de correlação entre os postos citados; e

n - número total de postos vizinhos considerados.

A soma de todos os fatores de peso deve ser a unidade.

Finalmente, o valor a preencher no posto Y é calculado empregando

(1.4)

A fim de simplificar a notação, foi suprimido o subíndice i nas observações dos postos vizinhos e no correspondente valor calculado.

Na aplicação deste método, sra adotado como critério mínimo o valor do coeficiente de determinação superior a 0,85 além da existência de, pelo menos, oito pares de eventos entre as estações para a realização da regressão.

As variáveis hidrológicas a serem analisadas neste estudo serão: vazões máximas diárias, caracterizadas pela freqüência; vazões mínimas diárias, caracterizadas pela duração e freqüência; vazões médias de longo período; precipitação pluvial média anual; precipitação pluvial do semestre mais chuvoso; e precipitação máxima diária anual.

Procedimentos semelhantes poderão ser utilizados no caso de serem escolhidas outras variáveis, como a evaporação e, ou, a temperatura média, que podem apresentar significância na regionalização.

Na obtenção das vazões máximas, serão usados os valores máximos diários anuais, enquanto que para a média de longo período será utilizado a média das vazões médias diárias anuais. Para as vazões mínimas serão utilizados os menores valores anuais, de sete dias de duração.

A vazão mínima anual de sete dias de duração será obtida computando-se, as médias móveis das vazões médias diárias com janelas de sete dias ao longo do ano civil. A mínima dessas médias é retirada. O processo será repetido para cada ano civil da série histórica, obtendo-se uma série de valores mínimos de vazões médias em sete dias consecutivos para cada ano.

As séries das vazões máximas e médias serão obtidas a partir dos registros fluviométricos do ano hidrológico.

Na regionalização das vazões máximas, será utilizado como variável independente a precipitação pluvial do semestre mais chuvoso ou a precipitação máxima diária anual para um determinado período de retorno. Já na regionalização das mínimas e da média de longo período será utilizada a precipitação pluvial média anual.

As características físicas de uma bacia são elementos de grande importância em seu comportamento hidrológico e podem apresentar pesos diferentes na regressão, de acordo com a região em estudo. Serão consideradas, neste estudo, as características físicas que mais explicam a distribuição da vazão e que sejam facilmente mensuráveis, como a área de drenagem da bacia, o comprimento e a declividade do curso d’água principal e a densidade de drenagem. A escala a ser adotada será a de 1:250.000.

O valor das áreas de drenagem das sub-bacias poderá ser obtido no Inventário das Estações Fluviométricas disponibilizado pela ANA, e na ausência deste dado ou quando seu valor apresenta dúvidas, torna-se necessário determiná-lo com auxílio de um planímetro ou por meio de sistemas de informações geográficas, caso a bacia tenha sido digitalizada. O processo de individualização das sub-bacias seguirá as regras conhecidas em hidrologia, sendo o traçado dos contornos das sub-bacias realizado unindo os pontos de máxima cota entre sub-bacias atravessando o curso d’água somente no ponto de saída. Os divisores de água topográficos separam as precipitações que caem nas sub-bacias.

O comprimento do curso d’água principal é aquele que drena a maior área no interior da bacia e, para sua obtenção será utilizado técnicas de geo-processamento

Para a estimativa da declividade média do curso d’água principal, foi utilizado o “método da declividade S1085”. A declividade S1085 (m/km) é obtida a partir da altitude a 10% e 85% do comprimento do curso d’água principal. A avaliação das altitudes nestes dois pontos, marcados nas cartas topográficas, é realizada por interpolação a partir das curvas de nível disponíveis. Avaliadas estas duas altitudes, a diferença entre elas, dividida por 75% do comprimento do curso d’água principal constitui a declividade S1085.

A densidade de drenagem fornece uma indicação da eficiência da drenagem da bacia. Este índice é expresso pela relação entre o comprimento total dos cursos d’água (sejam eles efêmeros, intermitentes ou perenes) de uma bacia pela sua área total. Denominando-se o comprimento total dos cursos d’água na bacia por L (km) e a área de drenagem por A (km²), a densidade de drenagem Dd (km/km²), adotada neste estudo, foi obtida por

(1.5)

Segunda etapa: Calcular a precipitação média nas sub-bacias

A segunda etapa compreende ao cálculo da precipitação média nas sub-bacias. Para o cálculo da precipitação média sobre as sub-bacias será utilizado o método de Thiessen. segundo o qual a precipitação média é calculada pela média ponderada entre a precipitação Pi, de cada estação, e o peso a ela atribuído Ai (área de influência de Pi), ou seja,

(1.6)

em que:

Pi - precipitação pluviométrica de cada estação;

Ai - área de influência da precipitação Pi.

Na versão 4.0 do programa computacional de regionalização hidrológica (RH4.0) foi desenvolvido um módulo para aplicação deste método. São exigidos como dados de entrada as coordenadas geográficas dos vértices dos polígonos que definem a bacia principal e todas as sub-bacias, além das coordenadas geográficas e do valor da precipitação média (no período considerado) de cada estação pluviométrica.

Este método atribui um fator de peso aos totais precipitados em cada aparelho, proporcionais à área de influência de cada um. Estas áreas de influência (pesos) são determinados em mapas da bacia contendo as estações, unindo-se os pontos adjacentes por linhas retas e, em seguida, traçando-se as mediatrizes dessas retas formando polígonos. Os lados dos polígonos são os limites das áreas de influência de cada estação.

De acordo com o aplicativo de regionalização hidrológica RH 4.0, são exigidos como dados de entrada as coordenadas geográficas dos vértices dos polígonos que definem a bacia principal e todas as sub-bacias, além das coordenadas geográficas e do valor da precipitação média (no período considerado) de cada estação meteorológica.

Os dados de entrada são os mesmos exigidos por outros métodos, entre eles o Método de Monte Carlo e o Método do Quadriculado, ressaltando-se apenas que o primeiro é um método estocástico enquanto que o segundo é determinístico. Ao receber estes dados, o programa exibe a representação gráfica, em escala, dos polígonos e das estações meteorológicas. Um exemplo desta representação gráfica pode ser observado na Figura 2, onde encontram-se representadas o contorno de uma bacia hidrográfica e seis estações meteorológicas.

Figura 2 – Exemplo da representação gráfica dos dados de entrada, para a descrição da metodologia

A precipitação média é calculada pelo método de Thiessen, segundo uma abordagem inteiramente analítica, que pode ser dividida em duas etapas (a e b):

a. Determinação das triangulações entre as estações meteorológicas

As triangulações são o conjunto de triângulos formados pela ligação, por segmentos retos, de três estações meteorológicas. Cada triângulo é determinado utilizando-se o seguinte princípio básico: nenhuma estação meteorológica pode estar no interior do círculo circunscrito neste triângulo. O centro deste círculo é um ponto notável do triângulo denominado ortocentro. Além disso, cada estação deve ser o vértice de pelo menos um triângulo. As triangulações assim definidas são denoninadas “Triangulações de Delaunay” e produzem um arranjo geometricamente único.

Seguindo-se este princípio, obtém-se, para o exemplo da Figura 2, as seguintes triangulações:

Figura 3 – Triangulações resultantes.

Qualquer arranjo geométrico diferente do arranjo da Figura 3 infringirá o princípio básico apresentado, como pode ser observado na Figura 4b, onde as estações 0 e 1 estão no interior dos círculos circunscritos nos triângulos 1-3-2 e 0-2-3, respectivamente.


(a)	(b)
Figura 4 – Exemplo de aplicação correta (a) e incorreta (b) do princípio da triangulação.

b. Cálculos Analíticos

b.1. Ordenação das triangulações

Este procedimento visa criar uma associação (ou lista) de todas as triangulações conectadas a cada estação, uma vez que as triangulações são criadas fora de ordem. Considerando que existam N estações meteorológicas e M triangulações definidas, então, para cada estação Ei (i=0,1...,N-1), o programa verificará em cada triangulação Mj (j=0,1...,M-1) se a estação Ei faz parte (é um dos seus vértices) da triangulação Mj; se fizer, associa Mj à estação Ei.

Ao final desta pesquisa, cada estação Ei terá uma associação de Ki (0 £ Ki £ N-1) triangulações dispostas desordenadamente ao seu redor. O próximo passo é ordenar as Ki triangulações associadas a cada uma das N estações. As estações que não foram incluídas em nenhuma triangulação, obviamente, não terão triangulações associadas.

O critério de ordenação é o ângulo formado entre o ponto de localização da estação e o ortocentro da triangulação, considerando-se o referencial trigonométrico. Estes ortocentros definem os vértices dos polígonos de Thiessen. As coordenadas (x, y) do ortocentro de um triângulo com vértices em (x₀, y₀), (x₁, y₁) e (x₂, y₂) podem ser calculadas pelas equações:

(1.8)

em que:

A = x₁ - x₀;

B = y₁ - y₀;

C = x₂ - x₀;

D = y₂ - y₀;

E = A (x₀ + x₁) + B (y₀ + y₁);

F = C (x₀ + x₂) + D (y₀ + y₂); e

G = 2 (A (y₂ - y₁) - B (x₂ - x₁)).

Com relação à Figura 3, em que N = 6 e M = 5, tem-se as seguintes triangulações associadas:

Estação	Antes da ordenação	Após a ordenação
0	{B, C, E}	{B, C, E}
1	{C, D, E}	{E, C, D}
2	{A, B, C, D}	{ B, A, C, D}
3	{E}	{E}
4	{A, B}	{A, B}
5	{A, D}	{A, D}

b.2 Cálculo das áreas dos polígonos de Thiessen

Para cada estação Ei, o programa calcula um polígono auxiliar Qi ligando, no sentido anti-horário, os ortocentros das triangulações associadas à estação Ei. Qi será um polígono fechado quando Ei for uma estação interna, como a estação 2. Se Ei for um estação de fronteira (0, 1, 3, 4 e 5) Qi deverá ser fechado, conforme a metodologia:

I. Arbitra-se um retângulo auxiliar, tal que contenha a bacia e todas as estações no seu interior.

II. Traça-se um segmento de reta do ortocentro da primeira triangulação, na direção perpendicular ao lado de fronteira, no sentido de dentro para fora, até interceptar o retângulo auxiliar.

III.Traça-se um segmento de reta do ortocentro da última triangulação, na direção perpendicular ao lado de fronteira, no sentido de dentro para fora, até interceptar o retângulo auxiliar.

IV.Acrescenta-se a interseção encontrada em (II); percorre-se o retângulo auxiliar no sentido anti-horário, acrescentando-se os seus vértices, até chegar a interseção encontrada em (III), que também deve ser acrescentada.

Figura 5 -Retângulo e polígonos auxiliares (linhas tracejadas), utilizados no cálculo dos polígonos de Thiessen.

O polígonos de Thiessen são calculados analiticamente por meio da interseção de cada polígono auxiliar Qi com o polígono que representa os limites da bacia. Um polígono de Thiessen será igual ao polígono auxiliar quando este estiver inteiramente no interior da bacia, terá uma área menor quando o polígono auxiliar interceptar os limites da bacia e, finalmente, terá área nula quando o polígono auxiliar estiver totalmente fora da bacia.

Figura 6 - Polígonos de Thiessen.

Finalmente, as áreas dos polígonos de Thiessen são calculadas pela fórmula genérica:

(1.9)

em que:

A_i = área do i-ésimo polígono de Thiessen;

n_i = número de vértices do i-ésimo polígono de Thiessen; e

x_k, y_k = coordenadas do k-ésimo vértice do i-ésimo polígono de Thiessen.

b.3. Cálculo da precipitação média

A precipitação média é calculada por meio da média ponderada:

(1.10)

em que:

Pm = precipitação média;

N = Número de estações meteorológicas;

P_i = precipitação média observada na i-ésima estação meteorológica; e

A_i = área de influência da i-ésima estação meteorológica.

Como ilustração, a Figura 7 apresenta os polígonos de Thiessen traçados e a localização das estações pluviométricas utilizadas, na Bacia do Alto São Francisco à montante da Barragem de Três Marias.

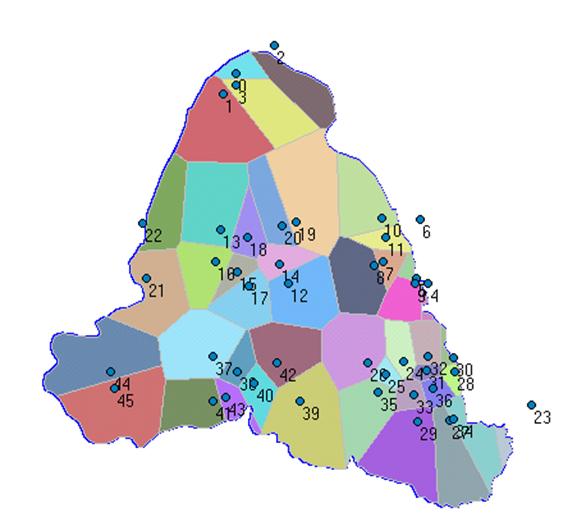Figura 7 -Polígonos de Thiessen da Bacia do São Francisco à montante da Barragem de Três Marias.

Terceira etapa: Identificar as regiões hidrologicamente homogêneas

Uma característica comum a toda as técnicas de regionalização é a utilização do conceito de região hidrologicamente homogênea. As regiões que subdividem uma área maior são escolhidas, teoricamente, com base na homogeneidade das características hidrológicas.

Na prática, a homogeneidade na regionalização é traduzida por um alto coeficiente de determinação, obtido da aplicação da regressão múltipla das vazões com as características físicas e climáticas das sub-bacias. Entretanto, a qualidade deste ajuste, mesmo procurando aplicar maior rigor no controle da regressão como coeficiente de determinação ajustado, erro padrão fatorial e teste F, o resultado pode ocultar ajustes inadequados ou tendenciosos devido ao número reduzido de graus de liberdade da regressão, principalmente quando se tem um número reduzido de estações (sub-bacias). Para evitar tais resultados deve-se procurar definir sub-regiões, nas quais as características das funções apresentem maior homogeneidade, representando, assim, melhor os eventos individuais.

Neste estudo, srão adotados dois critérios para definição das regiões hidrologicamente homogêneas, conforme apresentado em TUCCI (1993), ou seja:

a) Critério 1 - Baseado na análise da distribuição de freqüência das vazões adimensionalizadas de cada estação em papel probabilístico. O princípio em que se baseia este critério é que as distribuições de freqüências das vazões adimensionalizadas das estações em uma região hidrologicamente homogênea são idênticas. Essa característica permite que, ao se obter séries transformadas de vazões, através da divisão dos seus valores pelas respectivas médias, as distribuições de freqüência dessas séries transformadas sejam idênticas.

As distribuições de freqüência das séries de vazões serão representadas por distribuições teóricas de probabilidades, notadamente as distribuições log-normal, Gumbel e Weibull. Essa característica permite que o gráfico formado pelos pontos representativos dos valores de vazões, anotados em papel probabilístico adequado, seja o de uma linha reta. Desta forma, a equação da função distribuição de freqüências pode ser obtida, por regressão linear simples, pelo método dos mínimos quadrados.

A equação da reta de regressão da forma y = a + bx é ajustada às vazões adimensionalizadas de cada estação plotadas em papel probabilístico. Os valores de vazão são ordenados em ordem decrescente para as máximas e médias de longo período e crescente para as mínimas. Os parâmetros são estimados pelo método gráfico e o ajuste pelo método dos mínimos quadrados.

As estações que apresentarem valores do coeficiente de regressão linear “b” próximos deverão estar em uma região que, para efeitos de estudo, provavelmente deverá ser hidrologicamente homogênea.

b) Critério 2- É um critério estatístico baseado na análise do ajuste do modelo de regressão múltipla das vazões médias com as características físicas e climáticas das sub-bacias.

EUCLYDES et al. (1999) acrescenta que para a definição das regiões hidrologicamente homogêneas são analisados os coeficientes da regressão, a tendência e a classificação dos resíduos padronizados e o erro percentual entre os valores das vazões observadas e as estimadas pelo modelo.

A combinação de estações que apresentam o melhor ajustamento deverá estar, provavelmente, em uma região hidrologicamente homogênea.

A região será definida como hidrologicamente homogênea para as vazões estudadas se os dois critérios apresentarem bons resultados; se não, será necessário subdividir a região e reiniciar o processo.

Quarta etapa: Aplicar os métodos de regionalização de vazão

Neste estudo, serão aplicados dois métodos de regionalização, aqui denominados de Método 1 e Método 2, quais sejam:

a) Método 1 – Regionalização da vazão com determinado risco

Proposto por EUCLYDES (1992), consiste em ajustar distribuições teóricas de probabilidades às séries históricas de vazões de cada estação para diferentes períodos de retorno e, a seguir, aplicar regressão múltipla entre estas vazões e as características físicas e climáticas das sub-bacias.

Para representar os eventos máximos foram utilizadas as distribuições de Gumbel, Log-normal a dois e três parâmetros, Pearson tipo III e Log-Pearson tipo III, enquanto para os eventos mínimos serão as Log-normal a três parâmetros, Pearson tipo III, Log-Pearson tipo III e Weibull, por serem as mais recomendadas, para estes casos, na literatura (KITE, 1978; MAIONE, 1977; LETTENMAIR e BURGES, 1982; CRUFF e RANTZ, 1965).

As distribuições de freqüência são utilizadas para estimar a magnitude de eventos e, basicamente, existem duas fontes de erro ao utilizá-las. A primeira fonte de erro é que não se pode saber a priori qual das distribuições disponíveis é a "verdadeira" distribuição, ou qual distribuição os eventos seguem. Testes de aderência podem ser utilizados para escolher a distribuição que melhor descreve o comportamento dos eventos, mas isto não soluciona definitivamente o problema. Uma vez escolhida a função, a segunda fonte de erro torna-se evidente. Os parâmetros da distribuição de probabilidade devem ser estimados do conjunto de dados amostrais. Uma vez que a amostra de dados é sujeita a erros, o métodos de estimativa dos parâmetros deve minimizar estes erros e ser o mais eficiente possível.

Existem quatro métodos para a estimativa dos parâmetros das distribuições de freqüência: método dos momentos, método da máxima verossimilhança, método do quadrado mínimo e o método gráfico. Em ordem ascendente de eficiência os quatro métodos podem ser assim ordenados: gráfico, quadrado mínimo, momentos e máxima verossimilhança. Contrabalançando a sua grande eficiência, o método da máxima verossimilhança é de grande dificuldade para ser utilizado.

Para a maioria das distribuições de freqüência utilizadas em hidrologia, a estimativa da magnitude de um evento, com determinado período de retorno, pode ser colocada sob a forma da equação padrão de frequência devida a Vem Te Chow (KITE,1978):

X_T = m + K s (1.11)

em que

X_T- valor do evento com o período de retorno T;

m - média dos eventos amostrados;

s - desvio padrão dos eventos amostrados; e

K - fator de freqüência, depende da probabilidade e da assimetria.

Os valores do ator de freqüência (K), para as distribuições estudadas estão apresentados a seguir:

Distribuição Normal

K = t (1.12)

sendo,

em que,

t - desvio normal padronizado,

p - probabilidade de o evento ser menor ou igual x.

Distribuição Log-normal II

(1.13)

em que,

sendo,

(1.14)

– média da amostragem do evento x;

– desvio padrão da amostragem do evento x.

Distribuição Log-normal III

(1.15)

em que,

– coeficiente de assimetria

Distribuição Pearson III

(1.16)

Distribuição Log-Pearson III

Aplica-se a distribuição Pearson III aos logaritmos dos eventos amostrados.

Distribuição de Gumbel

(1.17)

em que,

T – período de retorno, anos.

Distribuição Weibull

(1.18)

sendo,

em que,

(1.19)

(1.20)

em que,

Ao se aplicar uma distribuição de probabilidade como modelo para descrever as vazões de um curso d’água deve-se testar a adequação deste procedimento, ou seja, verificar a boa ou má aderência dos dados da amostra ao modelo. Esta verificação é realizada por meio de testes de aderência como o teste do qui-quadrado, método de Kolmogorov-Smirnov e graficamente.

O teste de Kolmogorov-Smirnov (K-S) pressupõe que se duas sub-amostras são de uma mesma população, então a distribuição de probabilidade acumulada das duas sub-amostragens devem estar muito próximas. Se duas distribuições acumuladas são "muito discrepantes" em determinado ponto, então as sub-amostras podem ser de populações diferentes. Assim, um grande desvio é uma indicação para rejeitar-se a hipótese H_o (de serem da mesma população).

O teste K-S é baseado nos desvios da função de distribuição da amostra de eventos P(x) em relação à função de distribuição contínua escolhida P_o(x), assim:

D_n = max |P(x) - P_o(x)| (1.21)

O teste requer que o valor de D_n obtido seja menor que o valor tabelado para um determinado nível de confiança. Se o valor de D_n for maior que o valor crítico, rejeita-se H_o. Na Tabela 1, encontram-se os valores críticos para os níveis de significância usuais.

Tabela 1 - Valores críticos de Dn para o teste de Kolmogorov-Smirnov.

Tamanho amostra (n)	Nível de significância para D_n = max
Tamanho amostra (n)	α = 20%	α = 15%	α = 10%	α = 5%	α = 1%
1	0,900	0,925	0,950	0,975	0,995
2	0,684	0,726	0,776	0,842	0,929
3	0,565	0,597	0,642	0,708	0,828
4	0,494	0,525	0,564	0,624	0,733
5	0,446	0,474	0,510	0,565	0,669
6	0,410	0,436	0,470	0,521	0,618
7	0,381	0,405	0,438	0,486	0,577
8	0,358	0,381	0,411	0,457	0,543
9	0,339	0,360	0,388	0,432	0,514
10	0,322	0,342	0,368	0,410	0,490
11	0,307	0,326	0,352	0,391	0,468
12	0,295	0,313	0,338	0,375	0,450
13	0,284	0,302	0,325	0,361	0,433
14	0,274	0,292	0,314	0,349	0,418
15	0,266	0,283	0,304	0,338	0,404
16	0,258	0,274	0,295	0,328	0,392
17	0,250	0,266	0,286	0,318	0,381
18	0,244	0,259	0,278	0,309	0,371
19	0,237	0,252	0,272	0,301	0,363
20	0,231	0,246	0,264	0,294	0,356
25	0,210	0,220	0,240	0,270	0,320
30	0,190	0,200	0,220	0,240	0,290
35	0,180	0,190	0,210	0,230	0,270
> 35	1,07 √n	1,14 √n	1,22 √n	1,36 √n	0,63 √n

FONTE: HAAN, 1977.

No aplicativo de regionalização hidrológica RH4.0, é utilizado o método de Kolmogorov-Smirnov para testar os ajustes dos modelos probabilísticos. O aplicativo permite também a visualização gráfica das condições de ajuste da curva da distribuição aos dados observados.

b) Método 2 – Regionalização de curva adimensional de freqüência e do respectivo fator de adimensionalização

Consiste em adimensionalizar as curvas individuais de probabilidade, com base em seu valor médio, e estabelecer uma curva adimensional regional média das estações com a mesma tendência (TUCCI, 1993).

A curva adimensional regional de freqüência é expressa por

(1.22)

em que

Q_T = vazão estimada para período de retorno T e

Q_m = valor médio.

O valor médio é regionalizado em função das características físicas e climáticas das sub-bacias, utilizando-se, para isso, de uma equação de regressão múltipla, expressa por

Q_m = F₂ (A,L,Dd,...) (1.23)

em que F₂ ( A, L, Dd,..) = equação de regressão múltipla.

A curva adimensional regional de freqüência é determinada, ajustando-se a equação da reta de regressão da forma y = a + bx às vazões adimensionalizadas das estações pertencentes à região definida como hidrologicamente homogênea, plotadas em papel probabilístico. Os parâmetros são estimados pelo método gráfico e a verificação do ajuste é pelo método do mínimos quadrados. São aplicados limites de confiança de 95% e determinado o erro padrão de estimativa de freqüências com o auxílio da reta regional.

Conhecendo a equação de regressão múltipla da vazão média (Qmr) e através da curva de freqüência regional pode-se determinar QT/Qm para um risco T escolhido, e, em conseqüência o valor da vazão QT.

(1.24)

em que:

Q(T) - vazão máxima ou mínima estimada para período de retorno T;

(QT/Qm)R - termo adimensional da curva de freqüência regional para período de retorno T;

Qm - média aritmética das vazões máximas ou mínimas em cada estação, e

Qmr - vazão média máxima ou média mínima estimada pela equação de regressão múltipla.

Modelos de regressão múltipla utilizados

A análise de regressão investiga como as variações em uma ou mais variáveis independentes afetam a variação da variável dependente. A função matemática que relaciona as variáveis é da seguinte forma:

Q = F ( A, L, Dd, D, Pm) (1.25)

Utilizando-se, ou não, do artifício de transformação (transformação logarítmica, p. e.) pode-se aplicar vários modelos de regressão ao conjunto de dados. Os modelos utilizados são:

Modelo linear

Qm = βo + β₁.A + β₂.L + β₃ .Dd + β₄.d + β₅.Pm (1.26)

Modelo Potencial

Qm = βo A^β1 L^β2 Dd^β3 d^β4 Pm^β5 (1.27)

transformação utilizada:

lnQm = lnβ_o + β₁.lnA + β₂.lnL + β₃.lnDd + β₄.lnd + β₅.lnPm (1.28)

Modelo Exponencial

Qm = e^{(βo
+ β1.A + β2.L + β3.Dd + β4.d +
β5.Pm)} (1.29)

transformação utilizada:

lnQm = β_o + β₁.A + β₂.L + β₃.Dd + β₄.d + β₅.Pm (1.30)

Modelo Logarítmico

Qm = β_o + β₁.lnA + β₂.lnL + β₃.lnDd + β₄.lnd + β₅.lnPm (1.31)

Modelo Recíproco

Qm = (β_o + β₁.A + β₂.L + β₃.Dd + β₄.d + β₅.Pm)-1 (1.32)

transformação utilizada:

Qm-1 = β_o + β₁.A + β₂.L + β₃.Dd + β₄.d + β₅.Pm (1.33)

Uma série de avaliações objetivas pode ser realizada para se verificar a adequação do ajustamento de um determinado modelo aos dados. Entre estas avaliações serão adotadas o teste da função F, o valor do coeficiente de determinação e do desvio padrão dos erros do ajustamento, também chamado por erro padrão da estimativa.

1.2) METODOLOGIA DE REGIONALIZAÇÃO DA CURVA DE PERMANÊNCIA

Nem sempre o interesse do usuário da água está voltado para o conhecimento das vazões médias e máximas já apresentadas. Muitas vezes, o interesse consiste em conhecer a amplitude de variação das vazões e, principalmente, a freqüência com a qual cada valor de vazão ocorre numa determinada seção do curso d’água. A resposta para esta questão é encontrada através da curva de permanência das vazões em uma seção, pois, para cada vazão possível de ocorrência naquele local, associa-se a freqüência (ou número de vezes) com que ela é excedida.

A metodologia a ser adotada para estimativa da curva de permanência para cada estação fluviométrica, conforme TUCCI e CLARKE (2001), consistiu em:

- na seleção das séries de dados de vazões diárias foram utilizados apenas os anos das séries com mais de 95% dos dados diários de vazão, o que totaliza um mínimo de 347 dias;

- definição de 50 intervalos de classes das vazões diárias;

- sub-divisão dos intervalos de classe com base na escala logarítmica devido à grande variação de magnitude das vazões envolvidas;

- cáculo do intervalo de classe pela equação:

(1.34)

em que

Q_max - vazão máxima da série; e

Q_min - vazão mínima da série.

- cálculo dos limites dos intervalos. A partir de Q_min, adicionando o intervalo calculado anteriormente, o que resultará na vazão no limite superior do intervalo i :

(1.35)

- determinação, com base nos dados de vazão da série histórica de cada estação fluviométrica, do número de vazões classificadas em cada intervalo;

- determinação da frequência (f_i) associada ao limite inferior de cada intervalo:

(1.36)

em que

Nq_i - número de vazões de cada intervalo; e

NT - número total de vazões.

- obtenção da curva de permanência, plotando-se na ordenada os limites dos intervalos de classe de vazão e na abscissa a frequência de ocorrência.

A metodologia utilizada na regionalização compreenderá as etapas:

determinação da curva de permanência de cada estação fluviométrica;

determinação das vazões associadas a 50, 75, 80, 90 e 95% de permanência no tempo, a partir da curva de permanência obtida para as diferentes estações;

estabelecimento das equações de regressão para as probabilidades de 50% a 95%, com as características físicas da bacia e características da precipitação pluvial média anual;

a definição das regiões hidrologicamente homogêneas foi baseada na análise do ajuste do modelo de regressão múltipla da vazão para as probabilidades selecionadas com as características físicas e climáticas das sub-bacias.

Serão analisadas as significâncias dos coeficientes da regressão (teste T de Student, coeficientes de correlação e de correlação ajustado, erro padrão fatorial, coeficiente de variação e teste F ); como, também, a tendência e a classificação dos resíduos padronizados; e o erro percentual entre os valores das vazões observadas e as estimadas pelo modelo.

1.3) METODOLOGIA DE REGIONALIZAÇÃO DE CURVAS DE REGULARIZAÇÃO

Na literatura, sobre o assunto, existem diversos métodos para dimensionamento de reservatórios. Neste estudo, será utilizado o “método da curva de diferenças acumuladas”, conforme apresentado em LANNA (1993), para a determinação do volume de armazenamento necessário num reservatório para garantir uma determinada descarga máxima regularizada. Supõem-se nesta situação que se deseja determinar a menor capacidade útil de um reservatório suficiente para atender a maior demanda constante de água possível, num determinado período de anos.

Sendo a demanda constante ao longo do tempo ela será denotada por X. Pelo princípio de conservação de massa tem-se:

(1.37)

ou seja, o armazenamento inicial no açude (S₀), somado aos deflúvios afluentes ao açude durante um período de N intervalos de tempo (q_t), deve ser igual à soma das descargas retiradas do açude neste mesmo período, dada pelo produto (N.X), mais o armazenamento final (S_f). Supondo que o armazenamento inicial é idêntico ao final, ou que a diferença entre eles é pequena diante da soma das afluências, tem-se:

(1.38)

donde se conclui que a descarga máxima atingível nessas circunstâncias é:

(1.39)

Supondo que o açude tenha capacidade útil infinita, os armazenamentos em qualquer intervalo de tempo t serão dados por:

(1.40)

As diferenças acumuladas obtidas pela equação 1.40 mostram os acréscimos ou decréscimos dos armazenamentos no açude.

Conforme apresentado em TUCCI (1993), simulando a equação 1.40 para várias demandas pode-se obter a relação entre volume e vazão, ou seja:

V = f₁(q) (1.41)

em que

V - o volume; e

Q - vazão.

Modificando as variáveis envolvidas para

a = V/(Q_mlp 1ano) (1.42)

b = q/Q_mlp (1.43)

em que

Q_mlp - vazão média de longo período.

A função f₁ da equação 1.41 resulta numa função adimensional do tipo

a = f₂ (b) (1.44)

Com base nos valores obtidos da simulação pode-se ajustar uma função do tipo

a = a b^b (1.45)

cujos parâmetros a e b são obtidos por mínimos quadrados.

Esta expressão considera o atendimento de 100% da demanda durante a série histórica. Considerando que as curvas adimensionais da equação 1.45 são obtidas para cada estação, pode-se verificar a possibilidade de que estações de bacias com características semelhantes tenham a mesma tendência, já que as vazões mensais, que são as variáveis do processo, podem ser correlacionáveis.

A definição das regiões hidrologicamente homogêneas será baseada no coeficiente de determinação do ajustamento da curva regional e nos valores do coeficiente de regressão “b” obtidos no ajustamento da curva vazão versus volume. As estações que apresentarem altos valores do coeficiente de determinação da curva regional e valores próximos do coeficiente “b” deverão estar em uma região que, para efeitos de estudo, provavelmente deverá ser hidrologicamente homogênea.

Uso das curvas para estimativa de volume

Ao estimar o volume necessário visando à regularização da vazão, recomenda-se a seguinte sequência:

1) estima-se a vazão média de longo período (Q_mlp), utilizando o modelo de regressão múltipla da vazão média de longo período ajustado para a bacia;

2) sendo Q_reg a demanda desejada e Q_mlp a vazão média de longo período da região, calcula-se a demanda adimensional a ser regularizada (m)

m = (Q_reg/Q_mlp). 100 (1.46)

3) e de posse do valor calculado da demanda adimensional a ser regularizada (m), entra-se na equação da curva adimensional da região (Radim), em que se encontra a bacia, obtendo-se o seu valor:

Radim = (V/Q_m. 1ano).100 (1.47)

4) finalmente, o volume em hectometro cúbico (10⁶ m³) é obtido aplicando-se:

V = 0,3154. Radim. Q_mlp (1.48)

Para considerar a evaporação, pode-se utilizar uma metodologia simplificada, em que a evaporação é uma demanda adicional, em porcentagem (%), obtida por

me = 0,00317 E . A / Q_mlp (1.49)

em que,
E é a evaporação total média anual em mm; e A é a área do reservatório para 2/3 do seu volume útil, em km².

A demanda adicional total (m*), neste caso, é

m* = me + m (1.50)

Comentários:
a) No programa computacional de regionalização hidrológica, RH versão 4.0, foi desenvolvido um procedimento computacional para a regionalização das curvas de regularização, conforme metodologia apresentada. Para o traçado das curvas de regularização individuais, o programa identifica na série histórica de cada estação fluviométrica os valores da vazão mínima e da média e, a seguir, divide este intervalo em quinze pontos eqüidistantes. Considerando este procedimento na estimativa da capacidade de regularização, recomenda-se utilizar valores de (q/Qm)/100 dentro da faixa em que foi ajustada a curva regional;

b) A metodologia utilizada na simulação da estimativa do volume de acumulação (regionalização de curvas de regularização) considera que, caso exista vazões outorgadas à montante do barramento proposto, estas não são significativas a ponto de influenciar ou modificar a simulação do balanço hídrico do reservatório.

Exemplo de aplicação
Estimativa do volume de armazenamento para garantir uma vazão a ser regularizada de 400 L/s. As informações hidrológicas foram extraídas da Consulta espacial: "Modelos ajustados por curso d'água" válidos para o rio Turvo Sujo, localizado na bacia do rio Piranga/Doce (Figura 8) .

Figura 8 – Consulta espacial: "Modelos ajustados por curso d'água" válidos para o rio Turvo Sujo, localizado na bacia do rio Piranga/Doce.

Dados

Bacia	Rio Piranga/Doce
Sub bacia	Rio Turvo
Coordenadas	20º 45' S e 42º 05' W
Vazão de demanda	Qd = 0,40 m³/s
Vazão mínima	Q_7,10= 1,08
Vazão residual	(70% da Q_7,10) = 0,76 m³/s
Vazão a ser regularizada (Qreg = demanda + residual) *	0,40 + 0,76 = 1,16 m³/s
Vazão média de longo período	Q_mlp = 4,50 m³/s
Modelo da curva regional adimensional da região I	Radim = 1,26E-09 . (x)^5,73

* legislação ambiental: portaria do IGAM Nº 007/99.

Procedimentos:
1) Adimensionalizar a vazão a ser regularizada:

m = (Qreg / Qmlp). 100 (1.51)

m = (1,16 / 4,50) . 100 → m = 25,78 (1.52)

2) Substituir a vazão da demanda adimensional a ser regularizada (m) no modelo da curva regional adimensional (Radim) da Região I (Figura 8), cujo modelo apresenta a equação (em porcentagem):

Radim = 1,26E-09 . (x)^5,73 (1.53)

Radim = 1,26E-09 . (25,78)^5,73 → Radim = 0,15% (1.54)

3) Estimar o volume de acumulação (Hm³) utilizando a equação:

V = 0,3154 . Radim . Q_mlp(1.55)

V = 0,3154 . 0,15 . 4,50 → V = 0,21 Hm³ → V = 210.000 m³ (1.56)

Como ilustração do resultado da aplicação da “Metodologia de regionalização de curvas de regularização” extraído do banco de dados do programa computacional de regionalização hidrológica, RH versão 4.0, as Figuras 8a e 8b ilustram ajustes gráficos de: a) Curva de regularização adimensionalizada da estação fluviométrica de Ponte Nova jusante (código 56110005 - município de Ponte Nova), localizada no rio Piranga/Doce e b) Curva regional de regularização adimensionalizada dos rios pertencentes a Região I da bacia do rio Doce.

Figura 8a – Ajuste gráfico da curva de regularização adimensionalizada da estação fluviométrica de Ponte Nova (município de Ponte Nova), localizada no rio Piranga/Doce

Figura 8a – Ajuste gráfico da curva de regularização adimensionalizada da estação fluviométrica de Ponte Nova jusante (código: 56110005), localizada no rio Piranga/Doce

Fonte: RH versão 4.0

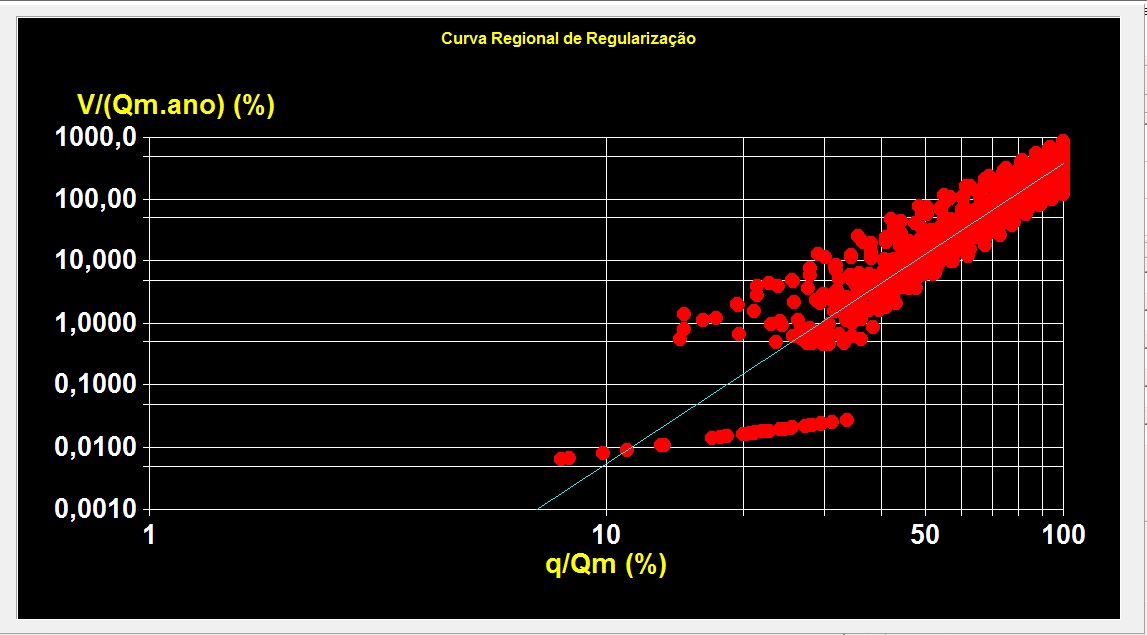Figura 8b – Ajuste gráfico da curva regional de regularização adimensionalizada dos rios pertencentes a Região I da bacia do rio Doce

Fonte: RH versão 4.0

2) METODOLOGIA DE MAPEAMENTO DAS VARIÁVEIS E FUNÇÕES HIDROLÓGICAS

O mapeamento de vazões específicas de uma bacia objetiva dar uma visualização da distribuição espacial das vazões média, máxima e mínima e permitir uma rápida estimativa da vazão específica desejada. No primeiro caso, um simples exame do mapa permitirá ao usuário ter uma noção das áreas carentes de água nos períodos de estiagem (vazão específica mínima), áreas sujeitas às maiores enchentes (vazão específica máxima) e disponibilidade de água da bacia (vazão específica média de longo período).

O mapeamento de vazões somente é possível através de vazões específicas, para que se possa compatibilizar valores de bacias de dimensões diferentes. A vazão específica é definida como sendo a vazão dividida pela área de drenagem da bacia.

Existe uma tendência geral das vazões específicas, principalmente a máxima, de reduzir com o aumento do tamanho da área de drenagem. Portanto, o mapa de vazões específicas é válido para um tamanho médio de bacia para o qual foi elaborado. Evidentemente, anomalias encontradas em algumas bacias poderão alterar esta tendência.

Como ilustração, a Figura 9 mostra a redução da vazão específica média máxima com o aumento da área de drenagem, nas três regiões hidrologicamente homogêneas identificadas nas sub-bacias do Alto e Médio São Francisco, em Minas Gerais.

Figura 8 – Vazão específica média máxima em função das áreas de
drenagem das sub-bacias do Alto e Médio São Francisco, em Minas Gerais.

Figura 9 – Vazão específica média máxima em função das áreas de drenagem das sub-bacias do Alto e Médio São Francisco, em Minas Gerais.

Quando na regionalização a vazão específica apresentar variabilidade com a área de drenagem da bacia, através de um modelo, não-linear, pode-se estimar a vazão para bacias com áreas de tamanho diferentes daquelas utilizadas no mapeamento, por meio da aplicação de um fator de correção, conforme recomendado por TUCCI (1999):

(1.57)

em que

fc - fator de correção;

A - área da bacia para a qual se deseja a vazão;

A_mapa- área da bacia utilizada na elaboração do mapa;

a - expoente da área da bacia na equação de regressão não-linear;

q_mapa - vazão específica obtida no mapa.

A estimativa da vazão de interesse pelo usuário (q) é obtida através do produto da vazão específica obtida no mapa pelo fator de correção, ou seja:

É importante ressaltar que a vazão estimada através destes mapas deve ser adotada como preliminar, pois o uso do modelo de regressão ajustado na regionalização permitirá estabelecer um valor mais confiável.

Neste estudo, será aplicada a seguinte seqüência de procedimentos para o mapeamento das vazões específicas:

1. digitalização dos cursos d’água principais e dos contornos das sub-bacias da região hidrográfica em estudo, em cartas geográficas planialtimétricas na escala de 1:250.000;

2. subdivisão desta região em sub-bacias com área de drenagem em torno de 500 km², permitindo uma variação de área de ± 15%.

3. determinação da vazão específica das sub-bacias com base no modelo de regressão ajustado para a região hidrologicamente homogênea identificada na regionalização;

4. locação dos valores das vazões específicas no centro de gravidade das sub-bacias; e

5. espacialização das vazões específicas, utilizando o ArcGis 9.3.1.

Como ilustração, as Figuras 10 e 11 mostram, na bacia do rio Doce, as localizações das sub-bacias com área de drenagem em torno de 500 km² e o mapa da vazão específica máxima diária anual para período de retorno de 50 anos, respectivamente.

Figura 9 – Localização das sub-bacias com área de drenagem em torno de 500 km2 na bacia do rio Doce.

Figura 10 – Localização das sub-bacias com área de drenagem em torno de 500 km² na bacia do rio Doce.

Figura 10 – Mapa da vazão específica máxima diária anual para período de retorno de 50 anos, na bacia do rio Doce.

Figura 11 – Mapa da vazão específica máxima diária anual para período de retorno de 50 anos, na bacia do rio Doce.

3) SISTEMA SIMPLIFICADO DE APOIO À GESTÃO DAS ÁGUAS – SAGA

Objetivando otimizar o procedimento ao estimar os valores das variáveis, funções e modelos hidrológicos obtidos nos estudos de regionalização hidrológica, será desenvolvida uma metodologia alicerçada em sistemas de informações geográficas, denominada Sistema Simplificado de Apoio à Gestão das Águas – SAGA

Este sistema possibilitará ao usuário, através de oito módulos de opção de consulta espacial georrreferenciada (8 por bacia e total de 88), obter informações hidrológicas diretamente sobre um mapa-base da hidrografia da bacia hidrográfica de interesse, apresentado na tela do monitor. São elas:

1. Informações hidrológicas na rede hidrográfica;

2. Informações em qualquer seção fluvial;

3. Modelos hidrológicos ajustados por cursos d’água;

4. Nascentes com informações hidrológicas;

5. Imagens de satélite;

6. Balanço demanda/disponibilidade por bacia;

7. Regiões hidrologicamente homogêneas;

8. Rede hidrológica georreferenciada com informações de vazão e precipitação pluvial.

No primeiro módulo – “Informações hidrológicas disponibilizadas na rede hidrográfica”, em cada “ponto de informação” a ser identificado na rede hidrográfica estará relacionada uma tabela de atributos, contendo o valor da área de drenagem da bacia e das variáveis e funções hidrológicas regionalizadas, para aquele ponto ou seção fluvial.

O procedimento a ser adotado para a geração e o armazenamento destas informações hidrológicas na rede hidrográfica será realizado basicamente em duas etapas:

A primeira etapa compreenderá a geração das informações hidrológicas, que basicamente constorá de um procedimento simplificado aplicado nos modelos de regressão ajustados nos estudos de regionalização hidrológica, desenvolvidos no âmbito do programa HIDROTEC. Serão adotados os seguintes critérios:

a área de drenagem da bacia será a variável considerada na regressão, em todos os modelos ajustados, e a precipitação média anual sobre as bacias, somente naqueles modelos que esta variável já estava inserida, e quando a sua retirada comprometeria significativamente o ajuste da regressão. É importante ressaltar que as variáveis área de drenagem e precipitação média anual são determinadas, automaticamente, com o auxílio de sistemas de informações geográficas e praticamente independem da escala do mapa utilizado na regionalização hidrológica. Por outro lado, as variáveis: comprimento do curso d’água principal, declividade do curso d’água principal e densidade de drenagem, dependem da escala do mapa utilizado na regionalização, que foi 1:250.000;

nos modelos de regressão em que as variáveis independentes: comprimento do curso d’água principal e,ou declividade do curso d’água principal e, ou, densidade de drenagem permaneceram na regressão, esta(s) será (serão) retirada(s) desde que a qualidade do ajustamento do modelo não ficasse comprometido. Será adotado como valor mínimo do coeficiente de determinação R2 ≥ 0,90;

quando não for possível a retirada das variáveis independentes, citadas anteriormente, sem comprometer a qualidade do ajustamento dos modelos de regressão múltipla (R2 <0,90), serão realizadas tentativas de correlações com a área da bacia e o comprimento do curso d’água principal como, também, da área da bacia com a densidade de drenagem, de forma a obter ajustes adequados em algumas regiões; e

nos modelos ajustados em que permaneceram, na regressão, a área da bacia e a precipitação média anual como variáveis independentes, será aplicado o programa computacional de regionalização hidrológica RH4.0 para calcular, automaticamente, os valores das áreas das sub-bacias estudadas e das precipitações médias sobre elas.

A segunda etapa constará do armazenamento das informações hidrológicas na rede hidrográfica digital, onde serão aplicados os seguintes procedimentos:

identificação e divisão dos cursos d’água principais em “pontos de informação” eqüidistantes de 10 km a partir das nascentes, utilizando-se como apoio, cartas topográficas planialtimétricas na escala de 1: 250.000;
digitalização dos cursos d’água principais e dos contornos das sub-bacias localizadas à montante de cada “ponto de informação”;
delimitação dos contornos das sub-bacias e identificação das coordenadas geográficas dos “pontos de informação” identificados na rede hidrográfica digitalizada (apoio: software AutoCad versão 2000);
estimativa dos valores das áreas de drenagem e da precipitação média sobre as bacias, em cada “ponto de informação” identificado na rede hidrográfica (apoio: software RH versão 4.0);
geração de tabelas, contendo os valores das variáveis hidrológicas, regionalizadas para cada “ponto de informação” (apoio: software EXCEL);
disponibilização das informações hidrológicas em cada “ponto de informação” identificado nos cursos d’água principais digitalizados (apoio ArcGIS 9.3.1).

Como ilustração, a Figura 12 mostra os cursos d’água principais da bacia do rio Doce, num total de 48, seccionados em 519 “pontos de informação” eqüidistantes de 10 km, a partir das nascentes, e a Figura 13 mostra os contornos das sub-bacias identificadas à montante dos referidos pontos.

Figura 11 – Cursos
d’água principais da bacia do rio Doce seccionados, em
“pontos de informação” eqüidistantes de 10 km, a partir das nascentes até a foz.

Figura 12 – Cursos d’água principais da bacia do rio Doce seccionados, em “pontos de informação” eqüidistantes de 10 km, a partir das nascentes até a foz.

Figura 12 – Contornos das sub-bacias identificadas à montante dos “pontos de informação”.

Figura 13– Contornos das sub-bacias identificadas à montante dos “pontos de informação”.

O segundo módulo – “Informações hidrológicas em qualquer seção fluvial” com funcionamento on-line (inédito no Brasil) o usuário identifica, no mapa da rede hidrográfica da bacia apresentada na tela do computador, o curso d’água de interesse (visualmente e com apoio de coordenadas geográficas) e após um clique com o mouse sobre a seção fluvial de interesse, o sistema determina, automaticamente, a área de drenagem da bacia e os valores das vazões máximas, médias e mínimas (Exemplo: Figura 14).

Figura 13 - Consulta espacial: Informações em qualquer seção fluvial da bacia do rio Paranaíba – MG

Figura 14 - Consulta espacial: Informações em qualquer seção fluvial da bacia do rio Paranaíba – MG

Alicerçado na tecnologia dos sistemas de informações geográficas - SIG’s, o sistema será desenvolvido com base nos modelos hidrológicos ajustados nas regiões hidrográficas mineiras no âmbito do programa HIDROTEC, na hidrografia digital do IBGE na escala de 1:250.000 e no modelo digital de elevação (MDE) obtido do projeto Shuttle Radar Topography Mission (SRTM), desenvolvido em escala mundial pela agência espacial americana (NASA), italiana (ASI) e alemã (DLR).

O terceiro módulo – “Modelos hidrológicos ajustados por curso d’água” será desenvolvido para ser utilizado nas situações em que a seção fluvial de interesse não coincidisse com os “pontos de informações” disponibilizados na rede hidrográfica digital.

Utilizando o ArcGIS 9.3.1 e respeitando-se os limites das regiões hidrologicamente homogêneas, identificadas na regionalização hidrológica, será possível ajustar modelos de regressão do tipo potencial em função da área de drenagem da bacia, utilizando-se os valores das variáveis e funções hidrológicas disponibilizadas nos “pontos de informação” da rede hidrográfica digital e proceder o armazenamento destes modelos na referida rede hidrográfica. Será adotado como valor mínimo do coeficiente de determinação R² >0,90.

Desta forma, para cada curso d’água identificado no mapa-base digital das regiões hidrográficas estudadas estará associado um modelo de regressão não linear, que poderá ser utilizado nas transferências e, ou, extrapolação espacial de informações hidrológicas.

A vazões e volumes de regularização em reservatórios serão estimados através dos modelos de regressão não linear ajustados, em função da área de drenagem da bacia, conforme os passos:

1. identificação no mapa da rede hidrográfica da bacia apresentada na tela do monitor, do curso d'água, onde se encontra a seção de interesse. Caso este curso d'água não esteja inserido no mapa, deve-se identificar o curso d'água mais representativo (afluente ou não) que servirá de base para a aplicação do modelo de regressão. Recomenda-se utilizar como apoio cartas geográficas em escalas menores daquela da região em estudo;

2. identificado o referido curso d'água e após um clique com o mouse sobre o mesmo, é apresentado na tela do monitor uma tabela de atributos, contendo informação sobre o intervalo válido das áreas de drenagem recomendado na regionalização hidrológica e os modelos de regressão ajustados para cada variável ou função hidrológica estudada;

3. finalmente, estima-se a variável ou função hidrológica desejada por meio da aplicação do modelo de regressão ajustado para o curso d'água de interesse, tendo como variável independente o valor da área de drenagem da sub-bacia identificada à montante do local da seção fluvial de interesse do usuário.

No quarto módulo - “Nascentes com informações hidrológicas” objetiva-se apresentar nessa consulta espacial um mapeamento das nascentes dos principais rios localizados em território mineiro com informações hidrológicas nos trechos dos cursos d'água considerados de 1º ordem segundo classificação de Strahler (segmentos de cursos d'água localizados entre uma confluência e uma nascente).

Figura 14 - Classificação dos
rios segundo Strahler

Figura 15 - Classificação dos rios segundo Strahler

A rede hidrográfica que compõe o banco de dados dessa consulta, denominada hidrorreferenciamento, foi desenvolvida pela Agência Nacional de Água (ANA). Corresponde a um conjunto de processos para o tratamento topológico da rede hidrográfica com base na codificação de Otto Pfafstetter (escala do milionésimo) a qual permite associar e extrair informações a jusante a montante de cada trecho.

Parâmetros cartográficos:

Representação cartográfica em sistemas de coordenadas geográficas;
Projeção cartográfica utilizada para cálculo das áreas de contribuição: projeção Equivalente de Albers;
Fonte da base cartográfica: Cartografia Sistemática ao Milionésimo;
Escala compatível - 1:1.000.000;
Sistema de referência - SAD69;
Estrutura- vetorial; e
Formato – shapefiles (ESRI).

As informações hidrológicas serão extraídas dos modelos hidrológicos ajustados nas regiões hidrográficas mineiras, no âmbito do programa HIDROTEC (disponibilizadas no website “Atlas Digital das Águas de Minas”).

O quinto módulo – “Imagens de satélite” será desenvolvido utilizando imagens de satélite do Google Maps de forma a permitir o confronto das informações hidrológicas (georreferenciadas) desenvolvidas no ATLAS com as paisagens presentes na bacia, tanto as de origem natural quanto devido a interferências antrópicas. Permitirá a visualização das seguintes informações digitais desenvolvidas no ATLAS: Informações hidrológicas na rede hidrográfica (pontos de informações hidrológicas eqüidistante 10 km das nascentes `a foz dos rios principais, seções fluviais com baixa capacidade de regularização natural, vazão dos afluentes principais, fotos e destaque da área da bacia sobre a imagem de satélite.

O sexto módulo – “Balanço demanda/disponibilidade por bacia” nas bacias hidrográficas estudadas será realizado com base em um índice determinado pela razão entre a vazão de retirada para usos consuntivos (vazão outorgada) e o limite outorgável no Estado de Minas Gerais (30% Q7,10). A vazão outorgada será extraída do cadastro de usuários outorgados disponibilizado no site do IGAM (rio Estadual) e ANA (rio federal), enquanto a vazão mínima de referência (Q7,10) será obtida em estudos de regionalização hidrológica realizados no âmbito do programa HIDROTEC.

O sétimo módulo – “Regiões hidrologicamente homogêneas” será obtido por meio de critérios físicos e estatísticos, baseados no escoamento superficial, características fisiográficas, distribuição de freqüência das vazões adimensionalizadas e nos resíduos da equação de regressão múltipla da vazão média conforme metodologia apresentada nesse trabalho e desenvolvida no aplicativo de regionalização hidrológica RH4.0.

O oitavo módulo – “Rede hidrológica georreferenciada com informações de vazão e precipitação pluvial” apresentará por região hidrográfica, a distribuição espacial das estações fluviométricas e pluviométricas disponibilizadas pela Agência Nacional das Águas – ANA (HidroWeb). Em cada estação, estará relacionada uma tabela de atributos contendo informações sobre sua localização (curso d’água ou município), coordenadas geográficas, período de dados da série histórica, código da estação, a área de drenagem e os valores das vazões máximas, médias e mínimas no caso de estação fluviométrica. Para estação pluviométrica será apresentado os valores da precipitação média anual, do semestre mais chuvoso e máxima diária anual.

No ATLAS a transferência espacial das informações hidrológicas será realizada por meio da aplicação de um dos procedimentos:

1. Transferência de informações da regionalização hidrológica → quando o valor da área de drenagem da bacia se encontrar dentro do intervalo utilizado na regionalização hidrológica; ou

2. Extrapolação espacial da regionalização hidrológica → quando o valor da área de drenagem da bacia se encontrar fora do intervalo utilizado na regionalização hidrológica

As “Consultas informativas" (13 por região hidrográfica e total de 143) corresponderá aos comportamentos hidrológicos mais relevantes a serem detectados em cada bacia hidrográfica por ocasião dos estudos hidrológicos. Apresentadas na forma de mapas, desenhos, figuras, tabelas e de textos elucidativos sobre estes, tornará muito interessante a comparação entre situações díspares dentro de uma mesma unidade hidrográfica. As metodologias de cada consulta estarão desenvolvidas nas respectivas páginas.

4) VALIDAÇÃO DAS METODOLOGIAS DESENVOLVIDAS NO ATLAS

4.1) VALIDAÇÃO DOS MODELOS HIDROLÓGICOS AJUSTADOS NAS REGIÕES HIDROLOGICAMENTE HOMOGÊNEAS IDENTIFICADAS NOS ESTUDOS HIDROLÓGICOS.

Será realizado um confronto entre os valores das vazões estimadas pelos referidos modelos e os valores das vazões estimados nas séries históricas de cinqüenta e oito (58) estações fluviométricas classificadas como "seções de controle”. Na Figura 16 observa-se a localização das "seções de controle" (estações fluviométricas) nas regiões hidrográficas estudadas. São elas:

Bacia do rio São Francisco - MG: Belo Vale e Paraopeba no rio Paraopeba; Carmo Cajuru e Velho da Taipa no rio Pará; Iguatama e Porto das Andorinhas no rio São Francisco; e Faz. Bom Jardim no rio Indaiá; Faz. Carvalho no rio São Domingos; Vila Urucuia e Barra do Escuro no rio Urucuia; Janaúba no rio Gurutuba; Boca da Caatinga no rio Verde Grande; Juvenilha no rio Carinhanha; Unaí e Santo Antônio Boqueirão no rio Preto; Ponte da BR – 040, Caatinga e Porto Alegre no rio Paracatu; Jequitibá, Piripama, Santo Hipólito e Várzea da Palma no rio das Velhas.

Bacia do rio Doce: Porto Firme no rio Piranga; Ferros no rio Santo Antonio; São Pedro do Suaçui no rio Suacui Grande; São Seb.da Encruzilhada (Pcd Inpe) no rio Manhuaçu; Cachoeira Escura, Governador Valadares (Pcd Inpe) e Linhares no rio Doce.

Bacia do rio Grande - MG: Aiuruoca no rio Aiuruoca; Porto Tiradentes no rio das Mortes; Itajubá no rio Sapucaí; Conceição dos Ouros no rio Sapucaí – Mirim; Conceição do Rio Verde no rio Verde; Uberaba e Conceição das Alagoas no rio Uberaba.

Bacias dos rios Jequitinhonha e Pardo: Vila Terra Branca, Barra do Salinas, Jequitinhonha (Pcd Inpe) e Itapebi no rio Jequitinhonha; Carbonita e Pega no rio Aracuai; Fazenda Benfica e Candido Sales no rio Pardo.

Bacias do Leste: Fazenda Cascata no rio Itanhem; Fazenda Diacui no rio Mucuri; Fidelândia e Boca da Vala no rio São Mateus.

Bacia do rio Paraiba Sul - MG: Tabuleiro no rio Formoso; Usina Brumado no rio Brumado; Sobraji no rio Paraibuna; Patrocinio do Muriaé no rio Muriaé.

Bacia do rio Paranaíba - MG: Fazenda Bom Jardim e Ponte Vicente Goulart no rio Paranaiba; Desemboque e Porto Saracura no rio Araguari; Fazenda Paraíso e Ituiutaba no rio Tijuco.

Figura 15 - Localização das 58 "seções de controle"
(estações fluviométricas) no mapa das regiões hidrográficas a serem estudadas.

Figura 16- Localização das 58 "seções de controle" (estações fluviométricas) no mapa das regiões hidrográficas a serem estudadas.

4.2) COMPARAÇÃO DAS CAPACIDADES DA VAZÃO DE PROJETOS/OBRAS HIDRÁULICAS IMPLANTADOS NO CAMPO E VAZÃO ESTIMADA NO WEBSITE DO ATLAS

Pretende-se realizar a comparação entre as seções de projetos de saneamento agrícola/urbano implantados pelo Fundação Rural Mineira - Ruralminas e monitorados no período de 1983 a 1993, como também a comparação entre as seções de obras hidráulicas implantadas no campo (extravasores de barragens, pontes vicinais, bueiros, etc) com as seções estimadas utilizando a metodologia a ser desenvolvida no “Atlas Digital das Águas de Minas”.

B) CONSIDERAÇÕES GERAIS SOBRE OS RESULTADOS

Por se tratar de um “Atlas” no formato de website (banco de dados eletrônico desenvolvido com o objetivo de democratizar o acesso e aumentar a capacidade de análise sobre um grande número de informações de uma extensa região hidrográfica), os resultados alcançados com informações mais detalhadas, encontram-se nos menus: “Panorama Hídrico”, “SAGA (Consulta Espacial Georreferenciada e Consulta Informativa)”, como também, em “Exemplos Aplicativos”.

Um resumo geral das metodologias de regionalização hidrológica aplicadas e resultados alcançados, encontra-se na opção “Consulta Informativa: Resumo Expandido" de cada bacia hidrográfica estudada.

Vale mencionar os modelos hidrológicos de vazões estatisticamente ajustados (e seus respectivos coeficientes de ajustamento) nas regiões hidrologicamente homogêneas (RHH) identificadas em cada bacia por ocasião dos estudos hidrológicos realizados. Estas informações estão contidas na "Consulta Informativa: Modelos ajustados nas RHH".

É importante comentar que os estudos hidrológicos de quantificações das vazões mínimas Q_7,10 ,Q₉₀ e Q₉₅ (georreferenciadas nas seções fluviais de toda a rede hidrográfica mineira, como também disponibilizadas em nível estadual, por bacia hidrográfica e por unidade de planejamento e gestão de recursos hídricos - UPGRH), desenvolvidos no âmbito do programa HIDROTEC objetivaram, também, fornecer informações importantes, ao orgão gestor estadual e aos comitês de bacias, sobre a disponibilidade hídrica encontrada em território mineiro de forma a permitir, aperfeiçoar num futuro próximo, estudos de vazões de referência diferenciadas para as regiões do Estado em função da significativa diversidade hidrológica existente em território mineiro, conforme pode-se observar no menu Panorama Hídrico "Ranking de produtividade hídrica".

Vale destacar os estudos de quantificação da vazão vazão mínima de sete dias de duração e período de retorno de 10 anos com intervalo sazonal (período seco – abril/setembro e período chuvoso – outubro/março) desenvolvidos no âmbito do programa HIDROTEC, em todo território mineiro, objetivando, também, fornecer alternativa ao orgão gestor estadual e aos comitês de bacias hidrográficas sobre uma nova proposta/critério de outorga a qual leva em consideração a sazonalidade das vazões. Em princípio recomenda-se a adoção dessa proposta somente nas regiões hidrográficas mineiras do "Baixo Rio Grande" e do rio Paranaíba tendo em vista o comprometimento dos recursos hídricos na calha principal dos dois rios com a geração de energia elétrica já instalada, como também, a demanda crescente de recursos hídricos para agricultura irrigada (importância socioeconômica e alto potencial agrícola existente nas respectivas regiões hidrográficas) já gerando conflitos de usos da água entre irrigantes em algumas sub-bacias. Informações mais detalhadas sobre esse tema encontra-se disponibilizado no menu Downloald do website HIDROTEC, denominada "Critério de outorga sazonal para agricultura irrigada no Estado de Minas Gerais - Estudo de caso",

É importante, também, registrar que os estudos de validação dos modelos hidrológicos para predição de vazão máxima em pequenas bacias ao se aplicar o procedimento "Extrapolação espacial da regionalização hidrológica" (bacias localizadas no limite inferior do intervalo válido para a regionalização hidrológica), apontaram para a adoção do período de retorno de 500 anos para as regiões hidrográficas dos rios Paranaíba e Grande em território mineiro e período de retorno de 100 anos para as demais regiões hidrográficas, incluindo aí, partes dos Estados do Espírito Santo, Bahia, Goiás e Distrito Federal inseridas no ATLAS.

Finalmente, é de fundamental importância documentar que os estudos realizados no ATLAS sobre o balanço hídrico das vazões outorgadas nas bacias hidrográficas mineiras, apresentadas na " Consulta espacial georreferenciada: Balanço entre demanda (vazão outorgada) e disponibilidade (30% do Q_7,10) por bacia" apontam para um esgotamento dos recursos hídricos outorgáveis em vários cursos d'água das bacias hidrográficas dos rios Verde Grande, Urucuia, Paracatu, Paranaíba, Jequitaí e com menor intensidade (apenas um curso d'água por bacia) nas bacias hidrográficas dos rios Doce (rio do Peixe), Mucuri (rio de todos os Santos), Paraopeba (rio Pardo) e Velhas (rio Bicudo).

Bibliografia

ATLAS digital das águas de Minas; uma ferramenta para o planejamento e gestão dos recursos hídricos. Coordenação técnica, direção e roteirização Humberto Paulo Euclydes. Belo Horizonte: RURALMINAS ; Viçosa : UFV, [2007] . 1 CD_ROM + manual (78p). ISBN 85.7601-082-8.

CRUFF, R.W.; RANTZ, S.E. A comparison of methods used in flood frequency studies for coastal basins in California, s.l., USGS Water Supply (Paper 1580-E ), 1965.

CUNNANE, C. Unbiased Plotting Positions – A Review. Journal of Hidrology, Amsterdam, v.37, p.205-222, 1978.

DRAPER, N. R.; SMITH, H. Applied Regression Analysis (2nd edition). Wiley, New York. GENSTAT 5 Committee, Rothamsted Experimental Station (1992). GENSTAT 5 Reference Manual. Clarendon Press, Oxford. 1981.

EUCLYDES, H. P.; PICCOLO, M.J. Aplicação de um critério de semelhança hidrológica pela distribuição de probabilidade de vazão de pico de cheia da Microregião do Circuito das Águas - Sul de Minas Gerais. Istituto di Idraulica e Construzioni Idrauliche del Politecnico di Milano, Itália, 1985. (Monografia).

EUCLYDES, H.P. Regionalização de vazões máximas e mínimas para a bacia do rio Juatuba-MG, Viçosa, UFV. Impr. Univ. 1992, 66p. (Tese M.Sc.).

EUCLYDES. H.P. et al. Regionalização hidrológica, manual do programa.Viçosa,MG: UFV / MMA /RURALMINAS, 1999.149p.

HAAN, C.T. Statistical methods in hydrology. 2ed. Ames, Iowa:The Iowa State University, Press/Ames, 1977. 378p.

HIDROTEC: Geração e transferência em recursos hídricos para o estado de Minas Gerais. Disponível em: <http://www.hidrotec.ufv.br>. Acesso em 12 de agosto de 2010.

IGAM: INSTITUTO MINEIRO DE GESTÃO DAS ÁGUAS. Legislação Estadual. Disponível em: <http://www.igam.mg.gov.br/leg_est.php>. Acesso em : 16 de maio de 2006.

KITE, G.W. Frequency and risk analyses in hidrology. Fort Collins, Water Resources,1978.224p.

LANNA, A. E. Regularização de vazões em reservatórios. In: TUCCI, C.E.M., org. Hidrologia. Porto Alegre, EDUSP, ABRH, 1993. p.703-720 (Coleção ABRH de Recursos Hídricos, 4).

LETTEENMAIER, D.P.; BURGES, S.J. Gumbel’s extreme value I distribution; anew look. Journal of the Hydraulics Division, v.108, p.502-513, 1982.

MAIONE, U. Aponti di idrologia - le piene fluviali. Pavia, La Goliarca Pavese. 1977, 224p.

RODRIGUEZ, E.: MORRIS, C.H.; BELZ, J.E. 2006. A global assessment of the SRTM performance. Photogrammetric Engineering and Remote Sensing, v.72, p.249-260.

RIBEIRO.C.A.S.; CHAVES. M.A.; SOARES.V.P.; EUCLYDES.H.P. Modelos Digitais de Elevação Hidrologicamente Consistentes para a Amazônia Legal. In: 2º Simpósio de Recursos Hídricos do Centro-Oeste. Campo Grande-MS:2002.

TUCCI, C.E.M.; CLARKE, R.T. Regionalização hidrológica. In: PAIVA, J.B.D.; PAIVA, E.M.C.D. (org.). Hidrologia aplicada à gestão de pequenas bacias hidrográficas. Porto Alegre: ABRH, 2001.p.169-222.

TUCCI, C.E.M. Regionalização de vazões. In: TUCCI, C.E.M. (org.). Hidrologia. Porto Alegre: EDUSP, ABRH, 1993.p. 573-611. (Coleção ABRH de Recursos Hídricos, 4).